Matlab: Points and vectors in 3D-plots

Points and Vectors in 3D-Plots

(German) This matlabfunction creates vectors and points for the previous post in the 3D cartesian coordinate system.

function punkt3D(x1,y1,z1,x2,y2,z2,sign,name,color,dx,dy,dz,true)

Therefor "startVec" are the initial values of the vector and "stopVec" the final values. You need the function (Cone/Arrow) and  (Grid3D). The optional arguments are shown below. For example you can use it as:

figure;hold on;axis off;

grid3D([0,0,0], [1,1,1], 'Amount', [4,4,4], 'Axes', gca, 'MinorGrid','Arrow','AxTicks',[{['']},{['']},{['']}],...

    'AxLabels',["";"";""]);

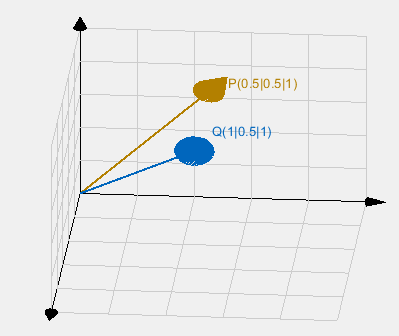
P = [0.5,0.5,1];

Q = [1,0.5,1];

point3D([0,0,0],P,'Marker','arrow','Label','P(0.5|0.5|1)','Color',[0.7 0.5 0]);

point3D([0,0,0],Q,'Marker','arrow','Label','Q(1|0.5|1)','Color',[0.0 0.4 0.74],'Deviation',[0,0,0.1]);

Souce code:

function point3D(startVec,stopVec,varargin)

% Input arguments:

% startVec ... input vector of the beginning of the point in [x,y,z]

% stopVec ... input vector of the ending of the point in [x,y,z]

%

% Optional input argument (varargin):

% 'Marker',sign ... defines the marker as '.' or 'arrow'

% 'LineWidth',LineWidth ... LineWidth of the vector

% 'Color',color ... define the color of the arrow/point

% 'Deviation',devVec ... defines the deviation to the point of the label

% 'Label',name ... defines the label of the point/arrow.

% 'PlotProjection' ... plot the projection from 0 to the point

    if isempty(varargin)

        varargin{1} = '';

    end

    

    [logic, index] = max(strcmp(varargin,'Marker'));

    if logic

        sign = varargin{index+1};

    else

        sign = '.';

    end

    

    [logic, index] = max(strcmp(varargin,'LineWidth'));

    if logic

        LineWidth = varargin{index+1};

    else

        LineWidth = 1.5;

    end

    

    [logic, index] = max(strcmp(varargin,'Color'));

    if logic

        color = varargin{index+1};

    else

        color = [0 0 0];

    end

    

    [logic, index] = max(strcmp(varargin,'Label'));

    if logic

        name = varargin{index+1};

    else

        name = '';

    end

    

    [logic, index] = max(strcmp(varargin,'Deviation'));

    if logic

        devVec = varargin{index+1};

        dx = devVec(1);

        dy = devVec(2);

        dz = devVec(3);

    else

        dx=0;

        dy=0;

        dz=0;

    end

       

    x1 = startVec(1); 

    y1 = startVec(2); 

    z1 = startVec(3); 

    x2 = stopVec(1);

    y2 = stopVec(2);

    z2 = stopVec(3);

    

    [logic, ~] = max(strcmp(varargin,'PlotProjection'));

    if logic

        plot3([0 x2],[y2 y2],[z2 z2],'--','Color',[0.8 0.8 0.8]);

        plot3([x2 x2],[0 y2],[z2 z2],'--','Color',[0.8 0.8 0.8]);

        plot3([x2 x2],[y2 y2],[0 z2],'--','Color',[0.8 0.8 0.8]);

    end

    if strcmp(sign,'arrow') == 1

        xrange = x2-x1;

        yrange = y2-y1;

        zrange = z2-z1;

        arrow3D([x2,y2,z2],[x2+xrange/7,y2+yrange/7,z2+zrange/7],'Length',1,'Thickness',1,'Color',color);

    else

        p2 = plot3(x2, y2, z2,sign,'Color',color,'Markersize',7);

    end

    p1 = plot3([x1 x2],[y1 y2],[z1 z2],'LineWidth',LineWidth);

    p3 = text(x2+x2/10+dx, y2+y2/7+dy, z2+z2/10+dz,name);

    set([p1 p3],'Color',color);

end